All Natural Numbers Are Either Happy or Sad. Some Are Narcissistic, Too

There are many different types of numbers, some of which you may remember from school: natural, rational, irrational, imaginary, calculable and incalculable numbers. Today, however, we are going to talk about something cheerful, namely, the “happy numbers.” Yes, they do indeed appear in mathematics, and that really is their technical name.

Happy numbers don’t have any real-world applications, but they do have amazing properties, which is why they are so popular among amateur mathematicians. For example, all natural numbers can be divided into either “happy” or “sad” numbers. And a generalization of “happiness” leads to the “narcissistic numbers,” which are strongly fixated on themselves.

Who first developed the concept of happy numbers is unclear. They were popularized by British mathematician Reginald Allenby in the 1960s: take any natural number, say, 13, square its digits (1² = 1; 3² = 9) and add them (1 + 9 = 10). Then repeat this happy calculation with the resulting number (1² + 0² = 1). If the sum of this second exercise is 1, you have reached a “fixed point.” That is, each further execution of the same process will always yield the result 1. Numbers that eventually yield a 1 by repeated happy calculations are called happy numbers.

[Read more about happy numbers]

Consequently, one would have to call all other numbers sad. The exciting thing is that the sad numbers also follow a fixed pattern when you apply the happy calculation. For example, let’s start with 4: 4² =16, and 16 will yield 37 (the sum of 1² = 1 and 6² = 36). If we keep this pattern going, we get 16 → 58 → 89 → 145 → 42 → 20 → 4. Because we started the happy calculation with 4, the number sequence starts over again. Thus, if the repeated happy calculation for a number yields the values 4, 16, 37, 58, 89, 145, 42 or 20, the number is bound to be sad. Allenby immediately wondered whether the natural numbers could all be split into happy (with end result of 1) or sad (part of the cycle starting with 4)—or whether the happy calculation has other endpoints.

There’s a quick way to find out. To do this, you first need to check just how large the sum of squared digits of a number can become. Suppose you have a one-digit number, say, 9. Its square, 81, is larger than itself. The same is true for two-digit numbers such as 99: 9² + 9² = 162. This is not true, however, for numbers with three or more digits. Even for 999, the sum of the squares of its digits is smaller than the number itself, namely, 243. This means that if you repeatedly perform the happy calculation for a three-digit number, you will only get three-digit values. If, on the other hand, you start with a four-digit number, the happy calculation in the first step will lead to a three-digit result.

An Algorithm for Sad Numbers

To prove that every natural number is either happy or sad, you have to go through all three-digit numbers. This task is tedious but not particularly complicated. For example, you can create a short algorithm to assist the process that follows these steps:

1. Choose a value from 0 to 9 for i, j and k.

2. Calculate z = i² + j² + k².

3. If z = 1, then the three-digit number ijk is a happy number.

4. If z = 4, 16, 37, 58, 89, 145, 42 or 20, then ijk is a sad number.

5. If neither case is true, set new values for i, j and k using the “floor function” Floor(x), which assigns each decimal number its rounded-down integer value (Floor(1.6) = 1): i = Floor(^z⁄₁₀₀), j = Floor(^{a – 100 x i}⁄₁₀), k = a – i x 100 – j x 10. With these new values for i, j and k, continue the algorithm at step 2.

Repeat this algorithm for all one-digit numerical values of i, j and k, and the result will always be either a happy or a sad number. In other words, all three-digit numbers are either happy or sad—as are all four-digit numbers because the sum of their squared digits (the first step in the happy calculation) will yield a three-digit number.

This argument can be continued for ever larger natural numbers. The result is that every natural number is either happy or sad. There is no value that escapes these fates when repeatedly using the happy calculation.

But experts were not satisfied with this result. Mathematicians have also wondered, for example, what percentage of numbers are happy. Do they become rarer with increasing size, like the prime numbers, or do they always appear with about the same frequency?

First, there are an infinite number of happy numbers. After all, every power of 10, 10^x, necessarily corresponds to a happy number.

But what about their density ρ, that is, the ratio of the happy to all natural numbers? Among the first 10 natural numbers, there are three happy ones (ρ = 0.3). Among the first 100, there are 20 (ρ = 0.2). And among the first 1,000 natural numbers, there are 143 happy ones (ρ = 0.143). There is even an entry in the Online Encyclopedia of Integer Sequences (OEIS) that deals only with the frequency of the happy numbers in an interval from 0 to 10ⁿ. Thus, if you calculate the density for different powers of n, you get the following picture:

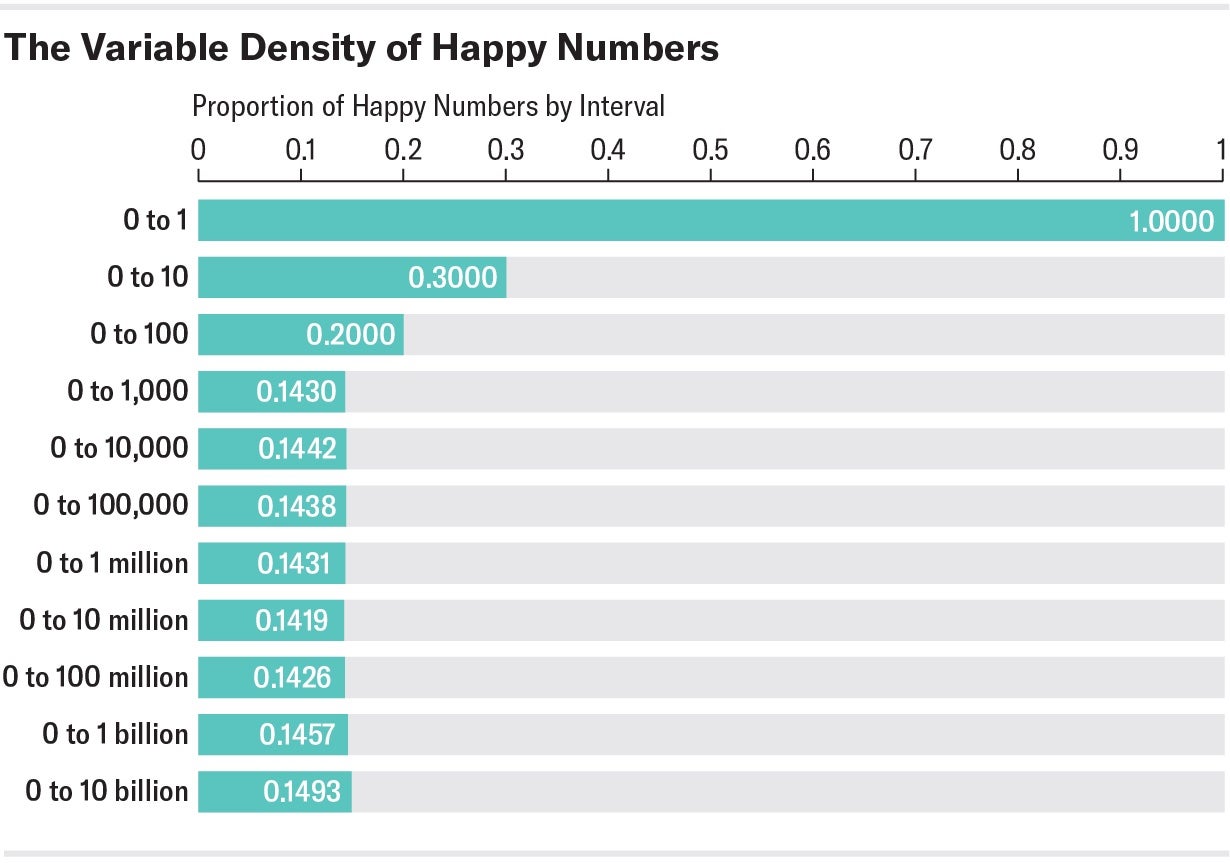
Now one might assume that the density is equivalent to about 14 percent. But as mathematician Justin Gilmer proved in 2011 in a preprint paper (which was then published in 2013), the happy numbers do not have a clearly defined density. Their density, he demonstrated, depends on the interval under consideration, and it does not converge to a fixed limit. Although that result surprised many people, the happy numbers are far from the only ones that do not have a fixed, defined density.

Such behavior is found, for example, in the set of all numbers beginning with a 1. Among the first nine numbers (1, 2, 3, 4, 5, 6, 7, 8, 9), there is exactly one that starts with a 1 (the number 1), which corresponds to a density of 1⁄9. Among the first 19 numbers (1, 2,…, 10, 11, 12,…, 19), there are 11 that start with a 1, giving a density of 11⁄19. And among the first 99 numbers, there are still 11 that start with a 1, so you have a density of 11⁄99 = 1⁄9 in this number interval. Among the first 199, there are 110 that start with 1, so the density is 110⁄199, and so on.

The density fluctuates between high and low values depending on which interval you pick. In such cases, no limit can be given for the density within the whole natural numbers. The same is true for the happy numbers. Depending on the interval, their density varies from a value below 12 to more than 18 percent.

Counting Consecutive Happy Numbers

Another question that keeps mathematicians occupied: How many consecutive happy numbers can there be? The first two are 31 and 32. To find the first three consecutive happy numbers, you must go to four-digit values: 1,880, 1,881, 1,882.

In a 2006 preprint paper, mathematician Hao Pan proved that there are any number of consecutive happy numbers. (The paper was subsequently published in 2008.) The catch is that you may have to search for a long time. A sequence with four consecutive numbers can be found at 7,839, one with five starts with 44,488, and one with six starts with 7,899,999,999,999,959,999,999,996.

Yet another puzzle is considering how many times the happy calculation is needed to bring a happy number to 1. This quantity can be used to define the overall happiness of a number. The fewer iterations, the happier the number. So 1, 10, 100, and so on are extremely happy, while 13 is slightly less so.

Which number is the least happy without being sad? Among the two-digit numbers, it’s 7. It takes five iterations to go from 7 to 1. Next up is 356, for which you need six passes of the happy calculation.

After that point, things get wild. If you want an even less happy number, you end up with a value of 977 digits: 378899999…999. The happy number with nine iterations has 10⁹⁷⁷ digits—and from the looks of it, there’s no limit to the number of iterations. One can find a happy number for any number n, which will yield a 1 only after n repeated happy calculations. Thus, there is no limit to the degree of nonhappiness.

And things become really exciting when one generalizes the concept of happy numbers. Instead of summing the squared digits, you can also add the third powers. In this case, the natural numbers no longer split into two camps but into nine. Either the iterations end at 1 (“happy cubes”), or they end at one of four other fixed points (153, 370, 371, 407) or in one of four cycles: 55 → 250 → 133 → 55; 160 → 217 → 352 → 160; 136 → 244 → 136; or 919 → 1,459 → 919.

Numbers That Return to Themselves

This generalization leads to another concept from number theory. When a number consists of n digits, you can calculate the sum of its digits exponentiated by n. For 243, for example, the result is: 2³ + 4³ + 3³ = 8 + 64 + 27 = 99. For some numbers, the result of this calculation leads back to itself. An example is 153 because 1³ + 5³ + 3³ = 153. Such numbers are called narcissistic.

All single-digit numbers are narcissistic. In fact, there are only 89 narcissistic numbers in total: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407, 1,634, 8,208, 9,474, 54,748, 92,727, 93,084, 548,834,… and the largest is 115,132,219,018,763,992,565,095,597,973,971,522,401.

It’s possible to prove that there are no narcissistic numbers larger than that with an estimation. Suppose a number has n digits. The maximum size of the summed digits raised to the power of n results if all digits have the value of 9: n x 9ⁿ. But above a certain size of n, this result is always smaller than the smallest number consisting of n digits (10^n–1). Thus, such a number cannot possibly be narcissistic.

The transition occurs with 60-digit numbers: while 60 x 9⁶⁰= 1.08 x 10⁵⁹ and is thus larger than 10⁵⁹, 61 x 9⁶¹= 0.99 x 10⁶⁰ and is smaller than 10⁶⁰. This is true for all n > 60. Therefore, there can be no narcissistic number consisting of more than 60 digits. By going through all numbers from 0 to 60 digits, one can test them for narcissism. As it turns out, there are only 89 of them.

Because there are only finitely many narcissistic numbers, they hold significantly fewer open questions than the happy numbers. But both categories are extremely suitable for an amusing pastime.

This article originally appeared in Spektrum der Wissenschaft and was reproduced with permission.