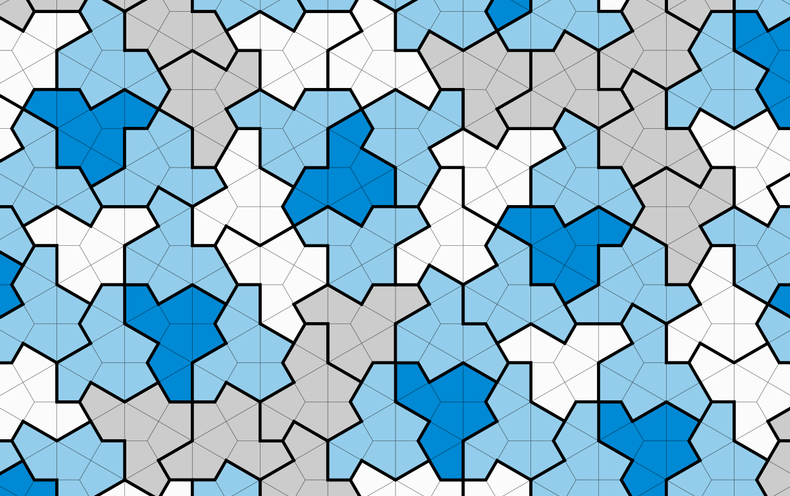
Creatively tiling a bathroom floor isn’t just a stressful task for DIY home renovators. It is also one of the hardest problems in mathematics. For centuries, experts have been studying the special properties of tile shapes that can cover floors, kitchen backsplashes or infinitely large planes without leaving any gaps. Specifically, mathematicians are interested in tile shapes that can cover the whole plane without ever creating a repeating design. In these special cases, called aperiodic tilings, there’s no pattern that you can copy and paste to keep the tiling going. No matter how you chop up the mosaic, each section will be unique.
Until now, aperiodic tilings always required at least two tiles of different shapes. Many mathematicians had already given up hope of finding a solution with one tile, called the elusive “einstein” tile, which gets its name from the German words for “one stone.”
Then, last November, retired printing systems engineer David Smith of Yorkshire, England, had a breakthrough. He discovered a 13-sided, craggy shape that he believed could be an einstein tile. When he told Craig Kaplan, a computer scientist at the University of Waterloo in Ontario, Kaplan quickly recognized the potential of the shape. Together with software developer Joseph Samuel Myers and mathematician Chaim Goodman-Strauss of the University of Arkansas, Kaplan proved that Smith’s singular tile does indeed pave the plane without gaps and without repetition. Even better, they found that Smith had discovered not only one but an infinite number of einstein tiles. The team recently reported its results in a paper that was posted to the preprint server arXiv.org and has not yet been peer-reviewed.
From Beautiful Patterns to Unprovable Questions
Anyone who has walked through the breathtaking mosaic corridors of the palace Alhambra in Granada, Spain, knows the artistry involved in tiling a plane. But such beauty harbors unanswerable questions—ones that are, as mathematician Robert Berger stated in 1966, provably unprovable.
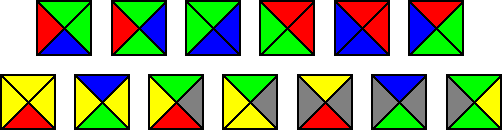
Suppose you want to tile an infinite surface with an infinite number of square tiles. You have to follow one rule, however: the edges of the tiles are colored, and only same-colored edges can touch.
With infinite tiles, you begin laying down pieces. You find a strategy you think is going to work, but at some point, you run into a dead end. There’s a gap you just can’t fill with the tiles you have available, and you are forced to place mismatched edges next to each other. Game over.
But certainly, if you had the right tile with the right color combination, you could have gotten out of your pickle. For example, maybe you needed just one tile in which all the edges were the same color. A mathematician would look at your game and ask, “Can you determine whether you will hit a dead end just by looking at the types of colored tiles you were given at the start? This would certainly save you a lot of time.”

The answer, Berger found, is no. There will always be cases where you can’t predict whether you can cover the surface without gaps. The culprit: the unpredictable, nonrepeating nature of aperiodic tilings. In his work, Berger found an unbelievably large set of 20,426 differently colored tiles that can pave a plane without the color pattern ever repeating itself. And even better, it is physically impossible to form a repeating pattern with that set of tiles, no matter how you lay them.
This discovery raised another question that has dogged mathematicians ever since: What is the minimum number of tile shapes that together can create an aperiodic tessellation?
How Low Can You Go?
In the decades that followed, mathematicians found smaller and smaller sets of tiles that can create aperiodic mosaics. First, Berger found one with 104 different tiles. Then, in 1968, computer scientist Donald Knuth found an example with 92. One year later mathematician Rafael Robinson found a variant with only six tile types—and finally, in 1974, physicist Roger Penrose presented a solution with only two tiles.
.png)
Then the progress stalled. Many mathematicians have since searched for the single-tile solution, the “einstein,” but none had succeeded—including Penrose, who eventually turned his attention to other puzzles. But David Smith, the 64-year-old retiree, hadn’t given up. He liked to play around with the PolyForm Puzzle Solver, a piece of software that lets users design and assemble tiles, according to the New York Times. If a shape looked promising, Smith cut out several paper puzzle pieces to experiment with. Then, in November 2022, he came across the now famous tile that he called the “hat” because of its top hat shape—though Kaplan emphasizes that many think it looks more like a T-shirt.
_webp.jpeg)
When Kaplan received an e-mail from Smith with the “hat,” it quickly piqued his interest. With the help of software, he lined up more and more hat-shaped tiles, and it seemed as if they might truly cover the plane without forming a repeating pattern.
But such a repeating pattern could still reveal itself if he kept laying down tiles—perhaps a redundant portion would only show up once the plane was several light-years long. The researchers needed to mathematically prove that the tiling was aperiodic. Kaplan turned to Myers and Goodman-Strauss, who had worked extensively with tiling in the past.
At first, they were amazed by the simplicity of the potential einstein tile because the “hat” has a fairly simple 13-sided shape. If you had asked Goodman-Strauss what an elusive einstein tile would look like before, “I would’ve drawn some crazy, squiggly, nasty thing,” he told Science News. And as the mathematicians took a closer look at the shape, they realized that they could play with the lengths of the sides and still create a seamless, aperiodic mosaic. This one shape had opened the door to an infinite number of einstein tiles.
A Never-Repeating Pattern
The mathematicians needed hard evidence to back up their claims. First, they used methods that experts have relied on for decades to show that certain kinds of tiles can create aperiodic mosaics. But Myers also went beyond these old methods to create a completely new way to prove it, which may also be useful for other tilings.
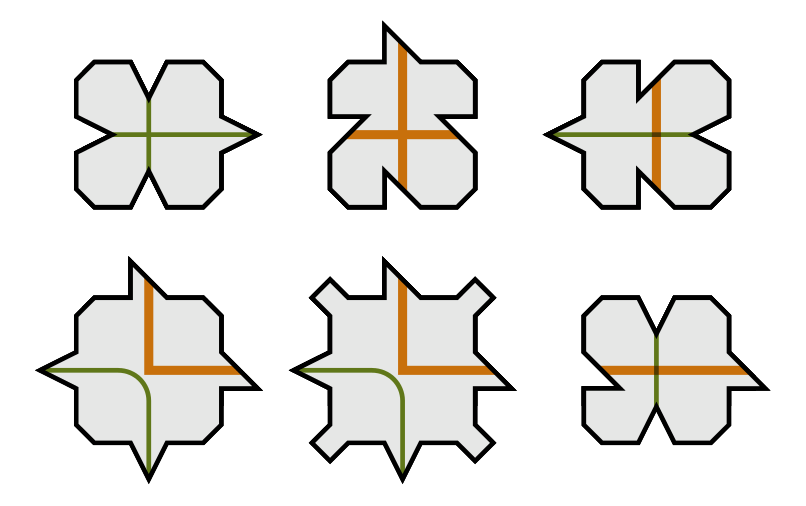
The tried-and-true method is best explained using Robinson’s six-tile set from 1969. The orange and green lines drawn on Robinson’s tiles function like the colored edges in the previous infinite-squares example. Here the rules are equally simple: two Robinson tiles can only be placed next to each other if the green and orange lines continue smoothly.
Following this rule results in a recognizable pattern consisting of larger and larger orange squares. If you keep zooming out, the squares continue to get bigger and intersect with one another. This builds up a hierarchical structure where each portion of the mosaic has its unique place. You can’t move or swap any sections without breaking the rules and destroying the structure. This tells us that the tessellation must be aperiodic.

Kaplan, Goodman-Strauss and Myers were able to show something similar for the hat-shaped einstein tile proposed by Smith. To make the tile easier to work with, they smoothed out the hat’s craggy edges into more recognizable and useful shapes—a single hat tile, for example, can be approximated with a triangle. They also used clusters of multiple einstein tiles to create different shapes. They could arrange four hat tiles into a hexagonlike structure, two tiles into a pentagon and another combination of two tiles into a parallelogram. These four smoothed-out shapes, which each consisted only of einstein tiles, could then completely cover the plane in a pattern.
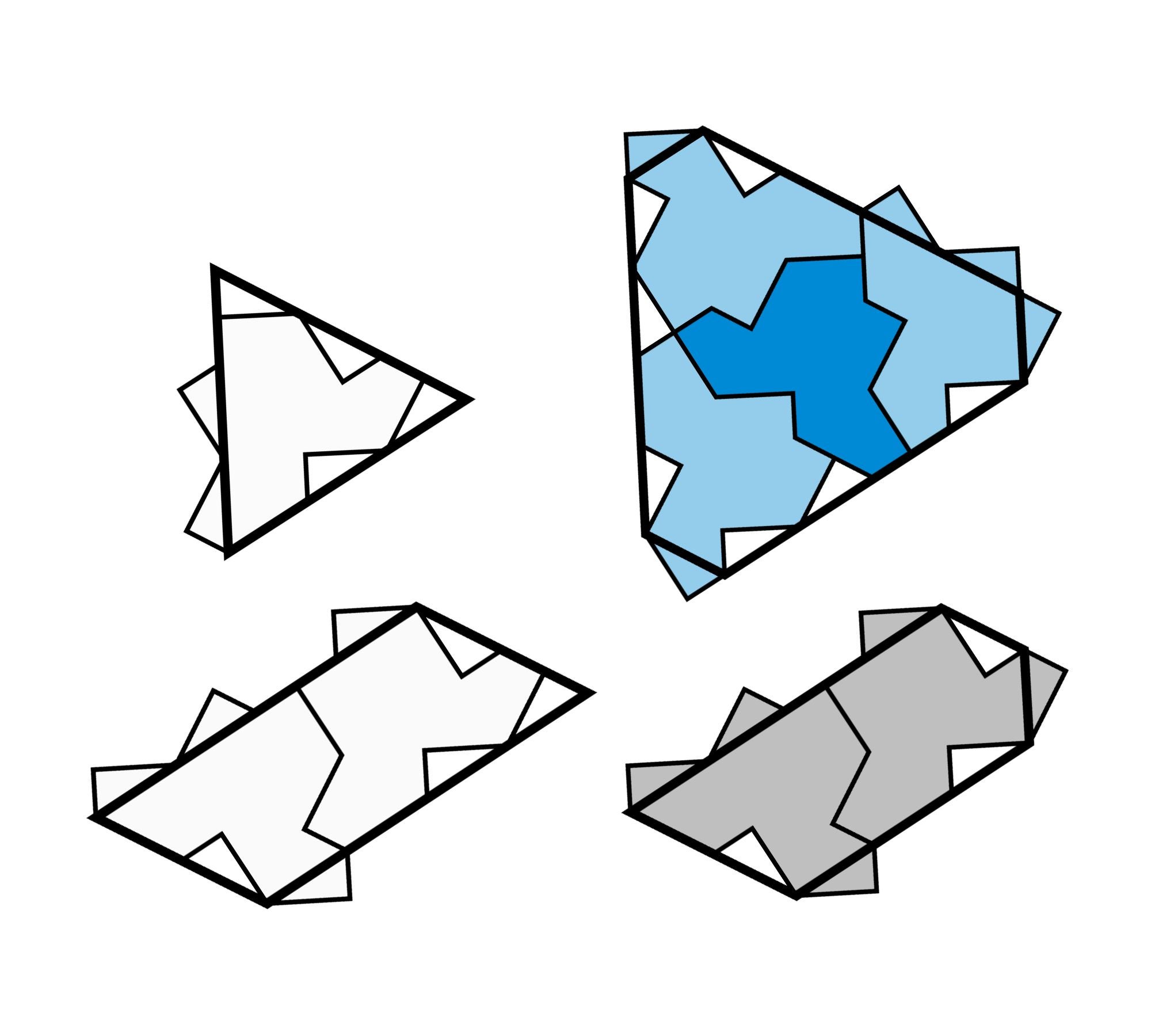
The mathematicians proved that this tiling contained no repeating patterns because, just like Robinson’s six-tile set, these four special shapes formed hierarchical structures. If you arrange these four einstein tile clusters (hexagon, pentagon, parallelogram and triangle) together, they will inevitably create a bigger version of one of those same shapes. Then, if you combine those larger shapes together, you’ll create even bigger versions of those shapes, and so on. This process can be repeated indefinitely, giving a hierarchical structure. Therefore, the overall pattern can’t be split into sections that repeat. If you simply slid portions of the pattern to another place, that overarching structure would be broken.
%5B2%5D_webp.jpeg)
Two Proofs Are Better Than One
This proof required some complex calculations, so the three scientists enlisted help from a computer. They released their computer-assisted proof freely so that anyone could check it for errors.
But Myers wasn’t satisfied yet. He created a new method for proving aperiodicity that could be performed by hand, without a computer, by showing that the einstein hat is connected to other well-known tilings that are easier to study. These related tilings are made of shapes called polyiamonds, simple tiles formed by combining equilateral triangles. Myers adjusted some of the einstein hat’s edges to form two different polyiamond arrangements that follow the hat’s same tiling pattern—one shaped like a chevron and the other like a hexagon and a rhombus put together. Despite their visual differences, these three arrangements all have the same properties. If the mathematicians could prove that both of the polyiamond tilings are aperiodic, then the original tiling must be aperiodic as well.
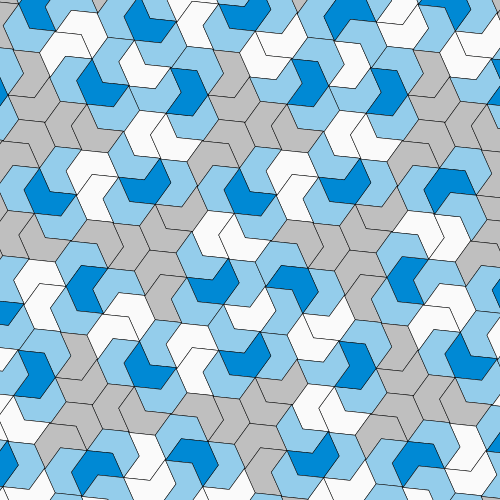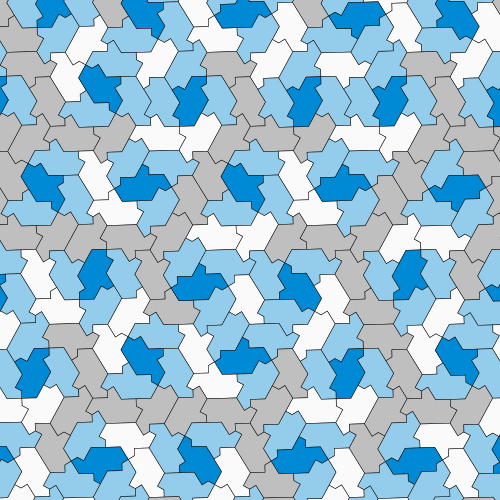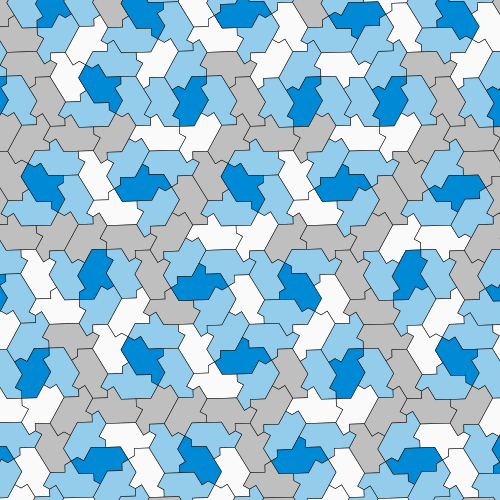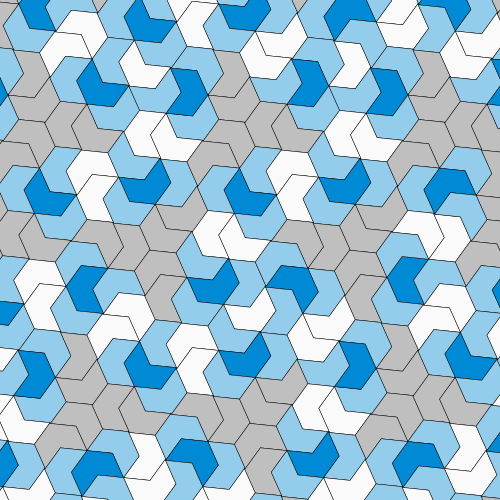
Thankfully, with polyiamonds, that proof is a matter of basic math. Mathematicians can represent the symmetries of polyiamond arrangements with a quantity called a translation vector. If the two new arrangements contained repeating patterns, the length of their translation vectors should have been related to each other—specifically, their ratio should have been a rational number. But instead the vectors had a ratio of the square root of 2—definitely an irrational number—showing that the polyiamond arrangements weren’t periodic. Therefore, the original hat tile was indeed an einstein.
Myers’s new proof method could also be helpful for other tilings, the scientists explain in their paper. But for now, both expert and amateur tilers are just excited to have the long-awaited einstein tile in hand. The home decor possibilities are literally infinite. As mathematician Colin Adams of Williams College told New Scientist, “I would put it in my bathroom if I were tiling it right now.”
This article originally appeared in Spektrum der Wissenschaft and was reproduced with permission.






























![‘911 Lone Star’ Season 5 Episode 8: Tommy’s Cancer Setback [VIDEO] ‘911 Lone Star’ Season 5 Episode 8: Tommy’s Cancer Setback [VIDEO]](https://tvline.com/wp-content/uploads/2024/11/911-lone-star-season-5-episode-8-tommy-cancer.jpg?w=650)